Центр Шпикера

Центр Шпикера
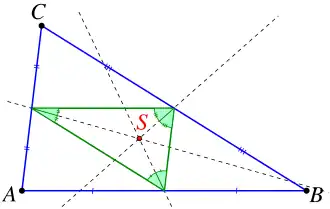Центр Шпикера есть инцентр серединного треугольника
Барицентрические координаты	${\displaystyle b+c:a+c:a+b}$
Трилинейные координаты	${\displaystyle {\frac {b+c}{a}}:{\frac {a+c}{b}}:{\frac {a+b}{c}}}$
Код ЭЦТ	X(10)
Связанные точки
Антидополнительная	центр вписанной окружности

Центр Шпикера — замечательная точка треугольника, определяемая как центр масс периметра треугольника; то есть центр тяжести однородной проволоки, проходящей по периметру треугольника^[1][2].

Точка названа в честь немецкого геометра XIX века Теодора Шпикера^[3]. В Энциклопедии центров треугольника Кларка Кимберлинга указана как X(10)^[4].

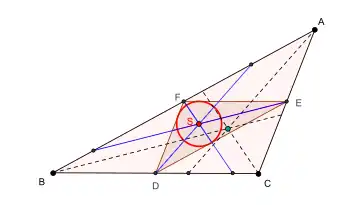
• Центр Шпикера является инцентром серединного треугольника^[1]. То есть центр Шпикера ${\displaystyle \triangle ABC}$ является центром окружности, вписанной в серединный треугольник ${\displaystyle \triangle ABC}$ (в его дополнительный треугольник)^[5]. Эта окружность известна как окружность Шпикера.

• Центр Шпикера является центром кливеров треугольника ${\displaystyle \triangle ABC}$^[1]. То есть все три кливера треугольника пересекаются в одной точке — в центре Шпикера ${\displaystyle S}$. (Кливер треугольника — это отрезок, один конец которого находится в середине одной из сторон треугольника, второй конец находится на одной из двух оставшихся сторон, при этом кливер разбивает периметр пополам.)

• Центр Шпикера, инцентр (${\displaystyle I}$), центроид (${\displaystyle G}$) и точка Нагеля (${\displaystyle M}$) треугольника лежат на одной прямой — на второй прямой Эйлера (прямой Эйлера — Нагеля). Более того^[6],

${\displaystyle \left\{{\begin{matrix}IS=SM;\\IG=2GS;\\MG=2IG.\end{matrix}}\right.}$

• Центр Шпикера лежит на гиперболе Киперта треугольника.

• Центр Шпикера ${\displaystyle \triangle ABC}$ является точкой пересечений прямых ${\displaystyle AX}$, ${\displaystyle BY}$ и ${\displaystyle CZ}$, где ${\displaystyle \triangle XBC}$, ${\displaystyle \triangle YCA}$ и ${\displaystyle \triangle ZAB}$ — подобные, равнобедренные и одинаково расположенные, построенные на сторонах треугольника ${\displaystyle \triangle ABC}$снаружи, имеющие один и тот же угол у основания ${\displaystyle \mathrm {arctg} \,\left(\mathrm {tg} \,{\frac {A}{2}}\;\mathrm {tg} \,{\frac {B}{2}}\;\mathrm {tg} \,{\frac {C}{2}}\right)}$^[7].
  • Это свойство выполняется не только для центра Шпикера. Например, первая точка Наполеона ${\displaystyle N_{1}}$, как и центр Шпикера, является точкой пересечений прямых ${\displaystyle AX}$, ${\displaystyle BY}$и ${\displaystyle CZ}$, где ${\displaystyle \triangle XBC}$, ${\displaystyle \triangle YCA}$ и ${\displaystyle \triangle ZAB}$ — подобные, равнобедренные и одинаково расположенные, построенные на сторонах треугольника ${\displaystyle \triangle ABC}$снаружи, имеющие один и тот же угол у основания ${\displaystyle 30^{\circ }}$.

• Центр Шпикера является радикальным центром трёх вневписанных окружностей^[8].
• трилинейные координаты точки ${\displaystyle S}$^[4]: ${\displaystyle (bc(b+c),\;ca(c+a),\;ab(a+b))}$.

• Барицентрические координаты центра Шпикера^[4]:

  ${\displaystyle (b+c,c+a,a+b)}$.

• Boris Odenhal. Some triangle centers associated with the circles tangent to the excircles // Forum Geometricorum. — 2010. — Т. 10.
• Theodor Spieker. Lehrbuch der ebenen Geometrie. — Potsdam, Germany, 1888.
• Ross Honsberger. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. — Mathematical Association of America, 1995.