Кактовикские цифры
Кактовикские цифры — система записи для используемой инупиатами Аляски двадцатеричной системы счисления.
Основание 20 в системе счисления используется во всех эскимосско-алеутских языках, и в том числе в инупиатском, при этом используется пятеричная база, то есть счёт ведётся с промежуточными отсчётами в точках 5, 10 и 15[1]. Арабские цифры, которые были разработаны для десятичной системы счисления, не подходят для языков инуитов. Чтобы решить эту проблему, учащиеся, живущие в городе Кактовик на Аляске, в 1994 году изобрели систему записи чисел[2], которая распространилась среди инупиатов[3].
Кактовикские цифры наглядно отражают лексическую структуру системы счисления народа инупиак. Например, число 7 на инупиаке называется tallimat malġuk («пять-два»), а кактовикская цифра для семи — это верхний штрих (пять), соединённый с двумя нижними штрихами (два): 
. Аналогично, двенадцать и семнадцать называются qulit malġuk («десять-два») и akimiaq malġuk («пятнадцать-два»), а кактовикские цифры — это соответственно два и три верхних штриха (десять и пятнадцать) с двумя нижними штрихами: 
, 
[4].
Значения
В таблице представлены десятичные значения кактовикских чисел до трёх знаков слева и справа от места единиц[4].
| n | n×20³ | n×20² | n×20¹ | n×20⁰ | n×20⁻¹ | n×20⁻² | n×20⁻³ |
|---|---|---|---|---|---|---|---|
| 1 |  , 8 000 |
400 |
20 |
1 |
. 0,05 |
. 0,0025 |
. 0,000125 |
| 2 |  ,16 000 |
800 |
40 |
2 |
. 0,1 |
. 0,005 |
. 0,00025 |
| 3 |  ,24 000 |
1 200 |
60 |
3 |
. 0,15 |
. 0,0075 |
. 0,000375 |
| 4 |  ,32 000 |
1 600 |
80 |
4 |
. 0,2 |
. 0,01 |
. 0,0005 |
| 5 |  ,40 000 |
2 000 |
100 |
5 |
. 0,25 |
. 0,0125 |
. 0,000625 |
| 6 |  ,48 000 |
2 400 |
120 |
6 |
. 0,3 |
. 0,015 |
. 0,00075 |
| 7 | , 56 000 |
2800 |
140 |
7 |
. 0,35 |
. 0,0175 |
. 0,000875 |
| 8 |  ,64 000 |
3200 |
160 |
8 |
. 0,4 |
. 0,02 |
. 0,001 |
| 9 |  ,72 000 |
3 600 |
180 |
9 |
. 0,45 |
. 0,0225 |
. 0,001125 |
| 10 |  ,80 000 |
4 000 |
200 |
10 |
. 0,5 |
. 0,025 |
. 0,00125 |
| 11 |  ,88 000 |
4 400 |
220 |
11 |
. 0,55 |
. 0,0275 |
. 0,001375 |
| 12 | , 96 000 |
4 800 |
240 |
12 |
. 0,6 |
. 0,03 |
. 0,0015 |
| 13 |  ,104 000 |
5 200 |
260 |
13 |
. 0,65 |
. 0,0325 |
. 0,001625 |
| 14 |  ,112 000 |
5 600 |
280 |
14 |
. 0,7 |
. 0,035 |
. 0,00175 |
| 15 |  ,120 000 |
6 000 |
300 |
15 |
. 0,75 |
. 0,0375 |
. 0,001875 |
| 16 |  ,128 000 |
6 400 |
320 |
16 |
. 0,8 |
. 0,04 |
. 0,002 |
| 17 | , 136 000 |
6 800 |
340 |
17 |
. 0,85 |
. 0,0425 |
. 0,002125 |
| 18 |  ,144 000 |
7 200 |
360 |
18 |
. 0,9 |
. 0,045 |
. 0,00225 |
| 19 |  ,152 000 |
7 600 |
380 |
19 |
. 0,95 |
. 0,0475 |
. 0,002375 |
Происхождение
В начале 1990-х годов во время дополнительных занятий по математике в школе Гарольда Кавеолука в Кактовике[2] ученики отметили, что в их языке используется двадцатеричная система счисления, и обнаружили, что с ними нельзя выполнять арифметические операции, так как арабские цифры не имеют достаточного количества символов для представления инупиакских чисел[5]. Ученики создали десять дополнительных символов, но обнаружили, что их трудно запомнить. В средней школе городка училось девять учеников. Их работой руководил учитель Уильям Бартли[5].
После мозгового штурма ученики выделили несколько качеств, которыми должна обладать идеальная система[5]:
- Визуальная простота: символы должны быть «легко запоминающимися».
- Наглядность: должна быть «чёткая связь между символами и их значениями».
- Эффективность: символы должны быть «лёгкими для написания», они должны «писаться быстро», без отрыва карандаша от бумаги.
- Своеобразие: они должны «сильно отличаться от арабских цифр», чтобы не возникало путаницы между обозначениями в двух системах.
- Эстетика: на них должно быть приятно смотреть.
В инупиакском языке нет слова, обозначающего ноль, и ученики решили, что кактовикская цифра 0 должна выглядеть как скрещённые руки, что означает, что ничего не считается[5].
Когда ученики начали преподавать свою новую систему младшим ученикам в школе, младшие ученики, как правило, сжимали числа, чтобы поместиться в блок такого же размера. Таким образом, они создали знаковую нотацию, в которой нижняя часть цифры 5 составляет верхнюю часть цифры, а остаток — нижнюю часть. Это оказалось визуально полезным при выполнении арифметических операций[5].
Вычисление
Счёты
Для своей системы счисления ученики создали счёты в школьной мастерской. Изначально они предназначались для помощи в преобразовании десятичной дроби в систему с основанием 20 и наоборот, но ученики обнаружили, что их конструкция вполне естественно поддаётся арифметике с основанием 20. В верхней части их счётов было по три костяшки в каждом столбце для значений подосновы 5, а в нижней секции было по четыре костяшки в каждом столбце для остальных единиц[5].
Арифметика
.svg.png)
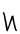
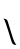(красный) входит в первые две цифры делимого один раз (синий) и один раз в частном (синий). Он умещается в следующие две цифры (подчёркнуты) один раз, но повёрнут (красный), поэтому следующая цифра в частном повёрнута на единицу (пять — красный). Последние две цифры совпадают один раз для получения последней в частном (белый)..svg.png)
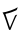
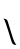
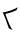входит в первые три цифры делимого дважды (обведены красным и синим), для двух в частном (красный и синий), в следующие три разряда (зелёный), не входит в следующие (ноль в частном), а в оставшиеся белые цифры один раз.Учащиеся обнаружили преимущество своей новой системы в том, что вычисления стали проще, чем с арабскими цифрами[5]. Сложение двух цифр будет выглядеть как их сумма. Например,
- 2 + 2 = 4
в кактовикской системе
- + =
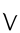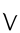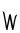
Вычитать ещё проще: нужно убрать необходимое количество штрихов, чтобы получить ответ[5].
Ещё одним преимуществом стало деление в длину. Визуальные аспекты и подоснова из пяти сделали деление больших чисел почти таким же простым, как деление коротких, поскольку не требовали записи в подтаблицах для умножения и вычитания промежуточных шагов[2]. Учащиеся могли отслеживать штрихи промежуточных шагов цветными карандашами в сложной системе разбиения на части[5].
Распространение
Кактовикские цифры получили широкое распространение среди инупиатов Аляски. Они были включены в программы языкового погружения и помогли возродить счёт по основанию 20, который выходил из употребления среди инупиатов из-за преобладания системы с основанием 10 в школах с английским языком обучения[2][5].
В 1995 году ученики средней школы Кактовика, которые изобрели эту систему, поступили в среднюю школу в Барроу (Аляска). Им разрешили преподавать эту систему ученикам местной средней школы, а местный колледж Игисавик добавил в свою учебную программу курс математики инуитов[5].
В 1996 году комиссия по истории, языку и культуре инуитов официально признала кактовикскую систему, а в 1998 году Совет инуитов в Канаде рекомендовал разработать и использовать эти числительные в своей стране[3].
Значение
Результаты Калифорнийского теста на успеваемость по математике в средней школе Кактовика в 1997 году резко улучшились по сравнению с предыдущими годами. После введения новых цифр их оценки стали выше средних по стране. Предполагается, что способность работать как десятичной, так и с двадцатеричной системами может дать заметные преимущества тем ученикам, которые имеют два образа мышления о мире[5].
Разработка собственной системы счисления помогает продемонстрировать учащимся из Аляски, что математика встроена в их культуру и язык, а не в западную культуру. Это отход от ранее распространённого мнения о том, что математика есть просто необходимость для поступления в колледж. Студенты-иностранцы могут увидеть практический пример иного мировоззрения, часть этноматематики[6].
Кодировка
Кактовикским цифрам присвоен блок в дополнительной многоязычной плоскости Unicode (U + 1D2C0-1D2DF)[7]. Эти изменения были приняты Техническим комитетом Unicode в апреле 2021 года и будут опубликованы как часть Unicode 15 в 2022 году. Они занимают диапазон от U + 1D2C0 (кактовикская цифра 0) до U + 1D2D3 (кактовикская цифра 19).
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| U+1D2Cx | 𝋀 |
𝋁 |
𝋂 |
𝋃 |
𝋄 |
𝋅 |
𝋆 |
𝋇 |
𝋈 |
𝋉 |
𝋊 |
𝋋 |
𝋌 |
𝋍 |
𝋎 |
𝋏 |
| U+1D2Dx | 𝋐 |
𝋑 |
𝋒 |
𝋓 |
Примечания
- ↑ MacLean (2014) Iñupiatun Uqaluit Taniktun Sivuninit / Iñupiaq to English Dictionary, p. 840 ff.
- 1 2 3 4 Bartley, Wm. Clark (January-February 1997). Making the Old Way Count (PDF). Sharing Our Pathways. 2 (1): 12–13. Архивировано (PDF) 25 июня 2013. Дата обращения: 27 февраля 2017.
{{cite journal}}: Википедия:Обслуживание CS1 (формат даты) (ссылка) - 1 2 Regarding Kaktovik Numerals.
- 1 2 MacLean (2014) Iñupiatun Uqaluit Taniktun Sivuninit / Iñupiaq to English Dictionary, p. 832
- 1 2 3 4 5 6 7 8 9 10 11 12 Bartley, William Clark. Perspectives on Indigenous People of North America. — Reston, Virginia : National Council of Teachers of Mathematics, 2002. — P. 225–236. — ISBN 978-0873535069.
- ↑ Engblom-Bradley, Claudette. The Alaska Native Reader: History, Culture, Politics. — Duke University Press, 2009. — P. 237–245. — ISBN 9780822390831. See in particular p. 244 Архивная копия от 22 мая 2021 на Wayback Machine.
- ↑ Roadmap to the SMP Архивная копия от 23 июня 2015 на Wayback Machine Unicode Inc., 2021.
Ссылки
- Grunewald, Edgar. Why These Are The Best Numbers! YouTube (30 декабря 2019). Дата обращения: 30 декабря 2019. The video demonstrates how long division is easier with visually intuitive digits like the Kaktovik ones; the illustrated problems were chosen to work out easily, as the problems in a child’s introduction to arithmetic would be.
- Silva, Eduardo Marín. Unicode request for Kaktovik numerals (L2/21-058R). Unicode Technical Committee Document Registry (29 апреля 2021). Дата обращения: 30 апреля 2021.