Точка Аполлония

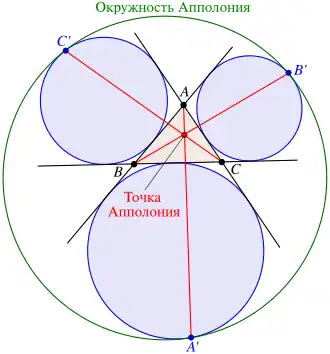
• Дан треугольник ${\displaystyle ABC.}$ Пусть вневписанные окружности треугольника ${\displaystyle ABC,}$ противоположные вершинам ${\displaystyle A,}$ ${\displaystyle B}$ и ${\displaystyle C,}$ есть соответственно ${\displaystyle E_{A},}$ ${\displaystyle E_{B},}$ ${\displaystyle E_{C}}$ (см. рисунок). Тогда окружность Аполлония ${\displaystyle E}$ (на рис. справа показана зелёным цветом) касается внутренним образом сразу трех вневписанных окружностей треугольника ${\displaystyle ABC}$ в точках соответственно ${\displaystyle E_{A},}$ ${\displaystyle E_{B}}$ и ${\displaystyle E_{C}}$ (см. рисунок)^[3].

• Решением упомянутой выше частной задачи Аполлония является указанная окружность ${\displaystyle E,}$ касающаяся трех данных окружностей ${\displaystyle E_{A},}$ ${\displaystyle E_{B}}$ и ${\displaystyle E_{C}}$ внешним образом.

Радиус окружности Аполлония равен ${\displaystyle {\frac {r^{2}+s^{2}}{4r}},}$ где ${\displaystyle r}$ — радиус вписанной окружности и ${\displaystyle s}$ — полупериметр треугольника^[4].

• Точка Аполлония ${\displaystyle Ap}$ или X(181) в энциклопедии центров треугольника, описанная в 1987-м году, определяется следующим образом:

Пусть ${\displaystyle A',}$ ${\displaystyle B'}$ и ${\displaystyle C'}$ есть точки касания окружности Аполлония ${\displaystyle E}$ с соответствующими вневписанными окружностями. Тогда прямые ${\displaystyle AA',}$ ${\displaystyle BB'}$ и ${\displaystyle CC'}$ пересекаются в одной точке ${\displaystyle Ap,}$ которую называют точкой Аполлония треугольника ${\displaystyle ABC.}$

• Ее трилинейные координаты:

${\displaystyle {\frac {a(b+c)^{2}}{b+c-a}}:{\frac {b(c+a)^{2}}{c+a-b}}:{\frac {c(a+b)^{2}}{a+b-c}}=}$

${\displaystyle =\sin ^{2}A\cos ^{2}({\frac {B}{2}}-{\frac {C}{2}}):\sin ^{2}B\cos ^{2}({\frac {C}{2}}-{\frac {A}{2}}):\sin ^{2}C\cos ^{2}({\frac {A}{2}}-{\frac {B}{2}}).}$