Волновая функция Лафлина

В физике конденсированного состояния волновая функция Лафлина^[1][2] представляет собой анзац, предложенный Робертом Лафлином для описания основного состояния двумерного электронного газа, помещённого в однородное магнитное поле в присутствии однородного фона электронного газа, когда фактор заполнения самого нижнего уровня Ландау равен ${\displaystyle \nu =1/n}$, где ${\displaystyle n}$ — нечётное положительное целое число. Она была построена для объяснения наблюдения состояния ${\displaystyle \nu =1/3}$ в дробном квантовом эффекте Холла (ДКЭХ) и предсказала существование дополнительных состояний ${\displaystyle \nu =1/n}$, а также квазичастичные возбуждения с дробным электрическим зарядом ${\displaystyle e/n}$, что позднее были подтверждены экспериментально. За это открытие Лафлин получил треть Нобелевской премии по физике в 1998 году.

Если игнорировать фон электронного газа и взаимное кулоновское отталкивание между электронами в приближении нулевого порядка, то мы имеем бесконечно вырожденный нижний уровень Ландау (НУЛ) и при коэффициенте заполнения 1/n можно было бы ожидать, что все электроны будут находиться на этом уровне. Включая взаимодействия, мы можем сделать приближение, что все электроны находятся на НУЛ. Если ${\displaystyle \psi _{0}}$ представляет собой одночастичную волновую функцию состояния НУЛ с наименьшим орбитальным угловым моментом, тогда анзац Лафлина для многочастичной волновой функции гласит

${\displaystyle \langle z_{1},z_{2},z_{3},\ldots ,z_{N}\mid n,N\rangle =\psi _{n,N}(z_{1},z_{2},z_{3},\ldots ,z_{N})=D\left[\prod _{N\geqslant i>j\geqslant 1}\left(z_{i}-z_{j}\right)^{n}\right]\prod _{k=1}^{N}\exp \left(-\mid z_{k}\mid ^{2}\right)}$

где координата обозначается как

${\displaystyle z={1 \over 2{\mathit {l}}_{B}}\left(x+iy\right)}$

в (гауссовых единицах)

${\displaystyle {\mathit {l}}_{B}={\sqrt {\hbar c \over eB}}}$

и ${\displaystyle x}$ и ${\displaystyle y}$ — координаты в плоскости xy. Здесь ${\displaystyle \hbar }$ — это приведённая постоянная Планка, ${\displaystyle e}$ — это заряд электрона, ${\displaystyle N}$ — общее число частиц, а ${\displaystyle B}$ — магнитное поле, перпендикулярное плоскости xy. Индексы z идентифицируют частицу. Для того чтобы волновая функция описывала фермионы, n должно быть нечётным целым числом. Это заставляет волновую функцию быть антисимметричной при обмене частицами. Угловой момент для этого состояния равен ${\displaystyle n\hbar }$.

Учитывать ${\displaystyle n=3}$ выше: результирующая ${\displaystyle \Psi _{L}(z_{1},z_{2},z_{3},\ldots ,z_{N})\propto \Pi _{i<j}(z_{i}-z_{j})^{3}}$ является пробной волновой функцией; она не точна, но качественно воспроизводит многие черты точного решения, а количественно имеет очень высокую схожесть с точным основным состоянием для малых систем. Предполагая кулоновское отталкивание между любыми двумя электронами, что основное состояние ${\displaystyle \Psi _{ED}}$ можно определить с помощью точной диагонализации^[3], а рассчитанные перекрытия близки к единице. Более того, при короткодействующем взаимодействии (псевдопотенциалы Холдейна для ${\displaystyle m>3}$ пренебрежимо малы), волновая функция Лафлина становится точной^[4], то есть ${\displaystyle \langle \Psi _{ED}|\Psi _{L}\rangle =1}$.

Волновая функция Лафлина — это многочастичная волновая функция для квазичастиц. Среднее значение энергии взаимодействия для пары квазичастиц равно

${\displaystyle \langle V\rangle =\langle n,N\mid V\mid n,N\rangle ,\;\;\;N=2}$

где экранированный потенциал

${\displaystyle V\left(r_{12}\right)=\left({2e^{2} \over L_{B}}\right)\int _{0}^{\infty }{{k\;dk\;} \over k^{2}+k_{B}^{2}r_{B}^{2}}\;M\left({\mathit {l}}+1,1,-{k^{2} \over 4}\right)\;M\left({\mathit {l}}^{\prime }+1,1,-{k^{2} \over 4}\right)\;{\mathcal {J}}_{0}\left(k{r_{12} \over r_{B}}\right)}$

где ${\displaystyle M}$ — конфлюэнтная гипергеометрическая функция и ${\displaystyle {\mathcal {J}}_{0}}$ — функция Бесселя первого рода. Здесь, ${\displaystyle r_{12}}$ — расстояние между центрами двух токовых контуров, ${\displaystyle e}$ — величина заряда электрона, ${\displaystyle r_{B}={\sqrt {2}}{\mathit {l}}_{B}}$ — ларморовский радиус, и ${\displaystyle L_{B}}$ — толщина электронного газа в направлении магнитного поля. Угловые моменты двух отдельных токовых петель равны ${\displaystyle {\mathit {l}}\hbar }$ и ${\displaystyle {\mathit {l}}^{\prime }\hbar }$, где ${\displaystyle {\mathit {l}}+{\mathit {l}}^{\prime }=n}$. Обратная длина экранирования определяется по формуле (в гауссовых единицах)

${\displaystyle k_{B}^{2}={4\pi e^{2} \over \hbar \omega _{c}AL_{B}}}$

где ${\displaystyle \omega _{c}}$ — циклотронная частота, а ${\displaystyle A}$ — площадь плоскости электронного газа в координатах xy.

Энергия взаимодействия оценивается как:

Для получения этого результата нужно произвести замену переменных интегрирования

${\displaystyle u_{12}={z_{1}-z_{2} \over {\sqrt {2}}}}$

и

${\displaystyle v_{12}={z_{1}+z_{2} \over {\sqrt {2}}}}$

и воспользоваться известным соотношением

${\displaystyle {1 \over \left(2\pi \right)^{2}\;2^{2n}\;n!}\int d^{2}z_{1}\;d^{2}z_{2}\;\mid z_{1}-z_{2}\mid ^{2n}\;\exp \left[-2\left(\mid z_{1}\mid ^{2}+\mid z_{2}\mid ^{2}\right)\right]\;{\mathcal {J}}_{0}\left({\sqrt {2}}\;{k\mid z_{1}-z_{2}\mid }\right)=}$

${\displaystyle {1 \over \left(2\pi \right)^{2}\;2^{n}\;n!}\int d^{2}u_{12}\;d^{2}v_{12}\;\mid u_{12}\mid ^{2n}\;\exp \left[-2\left(\mid u_{12}\mid ^{2}+\mid v_{12}\mid ^{2}\right)\right]\;{\mathcal {J}}_{0}\left({2}k\mid u_{12}\mid \right)=}$

${\displaystyle M\left(n+1,1,-{k^{2} \over 2}\right).}$

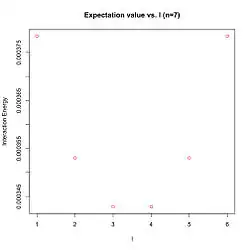
Энергия взаимодействия имеет минимумы для (рисунок 1) ${\displaystyle {{\mathit {l}} \over n}={1 \over 3},{2 \over 5},{3 \over 7},{\mbox{etc.,}}}$ и ${\displaystyle {{\mathit {l}} \over n}={2 \over 3},{3 \over 5},{4 \over 7},{\mbox{etc.}}}$

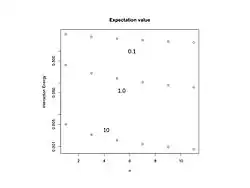
Для этих отношений угловых моментов энергия представлена на рисунке 2 как функция ${\displaystyle n}$.